6年生では「比」という新しい考え方を学習します。
比を使うと、2つの数量の関係をわかりやすく表したり、比べたりすることができます。
これまで学んだ「割合」の考え方を使いながら、等しい比を作ったり、比を簡単にしたりする方法を身に付けてけてほしいと思います。
比の値
比には「比の値」という考え方があります。
比の値は、前の数を後ろの数でわった商のことで、等しい比は同じ比の値になります。
3:4は、4分の3となります。
この性質を理解することで、等しい比をつくったり、比の関係を調べたりすることができるようになります。何度も挑戦し、迷わずに値を求められるようになってほしいです。
 比の値1 比の値1 |
 比の値2 比の値2 |
 比の値3 比の値3 |
 比の値4 比の値4 |
 比の値5 比の値5 |
 比の値6 比の値6 |
 比の値7 比の値7 |
 比の値8 比の値8 |
 比の値9 比の値9 |
比を簡単にする(整数の比)
比を できるだけ小さい整数の比に直すことを「比を簡単にする」といいます。
比の性質を使って、比を簡単にする方法を身に付けてほしいです。
九九の答えを思い出して取り組んでほしいです。
 比を簡単にする1 比を簡単にする1 |
 比を簡単にする2 比を簡単にする2 |
 比を簡単にする3 比を簡単にする3 |
 比を簡単にする4 比を簡単にする4 |
 比を簡単にする5 比を簡単にする5 |
 比を簡単にする6 比を簡単にする6 |
少し難しい問題です。
 比を簡単にする7 比を簡単にする7 |
 比を簡単にする8 比を簡単にする8 |
 比を簡単にする9 比を簡単にする9 |
 比を簡単にする10 比を簡単にする10 |
 比を簡単にする11 比を簡単にする11 |
 比を簡単にする12 比を簡単にする12 |
比を簡単にする(小数・分数の比)
比が小数や分数で表されているときも、整数の比に直してから簡単にすることができます。
小数第1位の小数の比は10倍にして整数に直し、分数の比は通分してから分母をはらって整数に直します。
いろいろな形の比を、簡単な整数の比で表せるようになってほしいと思います。
 比を簡単にする1 比を簡単にする1 |
 比を簡単にする2 比を簡単にする2 |
 比を簡単にする3 比を簡単にする3 |
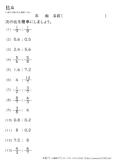 比を簡単にする4 比を簡単にする4 |
 比を簡単にする5 比を簡単にする5 |
 比を簡単にする6 比を簡単にする6 |
 比を簡単にする7 比を簡単にする7 |
 比を簡単にする8 比を簡単にする8 |
 比を簡単にする9 比を簡単にする9 |
比の一方の値を求める文章題
「赤と青のテープの長さの比が2:3で、赤のテープが6cmのとき、青のテープは何cmでしょう」
このように、比と一方の値がわかっているときに、もう一方の値を求める問題に挑戦します。
対応する比を考え、問題を解いてほしいです。
 比の片方の値を求める1 比の片方の値を求める1 |
 比の片方の値を求める2 比の片方の値を求める2 |
 比の片方の値を求める3 比の片方の値を求める3 |
 比の片方の値を求める4 比の片方の値を求める4 |
 比の片方の値を求める5 比の片方の値を求める5 |
 比の片方の値を求める6 比の片方の値を求める6 |
全体の量を比例配分する文章題
「60個のあめを、姉と妹に2:3の比で分けます。それぞれ何個ずつになるでしょう」このように、全体の量を比の関係に合わせて分けることを「比例配分」といいます。
日常生活でもよく使う大切な考え方ですので、しっかりと身に付けてほしいと思います。
 全体の量を比例配分1 全体の量を比例配分1 |
 全体の量を比例配分2 全体の量を比例配分2 |
 全体の量を比例配分3 全体の量を比例配分3 |
 全体の量を比例配分4 全体の量を比例配分4 |
 全体の量を比例配分5 全体の量を比例配分5 |
 全体の量を比例配分6 全体の量を比例配分6 |


